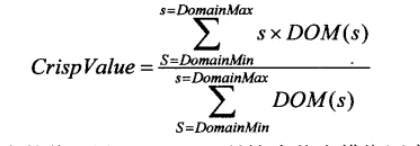《游戏人工智能编程案例精粹》学习笔记（三）

关于《游戏人工智能编程案例精粹》的学习笔记。本节主要是模糊集合的介绍以及模糊逻辑的应用。

模糊集合

普通集合适用于一些非黑即白的情况，而实际情况通常有一些模棱两可的情形需要考虑。这时就需要引入模糊集合，仅为引入模糊逻辑所需，不作过多展开。

概念

给定一个论域U，那么从U到单位区间 [0,1] 的一个映射 μ：U->[0,1] 称为U上的一个模糊集合，或U的一个模糊子集。

其中映射称为隶属函数，对于特定元素，该映射的值称为隶属度。通常简单的隶属函数为三角形或梯形。传统集合的隶属度则为0或1，也即属于或不属于。
这一概念由美国加利福尼亚大学控制论专家L.A.扎德于 1965 年率先提出，适用于我们熟悉的秃头悖论等玄学问题。

运算

设A与B是同一论域U上的两个模糊集合。

模糊集合的包含：

A ⊂ B 即 μ_A(u) ≤ μ_B(u) ∀ u ∈ U 模糊集合的等于： A = B 即 μ_A(u) = μ_B(u) ∀ u ∈ U 模糊集合的并集运算： μ_{A ∪ B}(u) = max { μ_A(u) , μ_B(u) } 模糊集合的交集运算： μ_{A ∩ B}(u) = min { μ_A(u) , μ_B(u) } 模糊集合的补集运算： μ_A`(u) = 1 - μ_A(u)

基本运算定律

模糊集合的运算同样满足恒等律，交换律，结合律，分配律，吸收律，同一律，对偶律等定律，不同的是互补律不满足，也即：

A ∩ A` ≠ Ø A ∪ A` ≠ E 此处E为模糊全集，满足 μ_E(u) = 1 ∀ u ∈ U Ø为模糊空集，满足 μ_Ø(u) = 0 ∀ u ∈ U

限制词

限制词是一元运算符，用于修饰模糊集合的含义，常用的修饰词例如“极”，“非常”，“略”，“稍微”。对于一个模糊集合来说，这些修饰词的含义通常为对模糊集合的隶属度函数取平方或开根号。
例如，如果定义模糊子集“老”的隶属度函数为μ_老(u)，且修饰词的隶属度函数如下：

μ_极A = μ_A⁴ μ_非常A = μ_A² μ_略A = μ_A^0.5 μ_稍微A = μ_A^0.25 则有 μ_极老(u) = μ_老⁴(u) μ_非常老(u) = μ_老²(u) μ_略老(u) = μ_老^0.5(u) μ_稍微老(u) = μ_老^0.25(u) 这是非常直观的，因为集合使用这些修饰词后，标准也就应当比原先更为宽松或严格。

模糊数

连续论域U上的模糊数F是一个U上的正规凸模糊集合。其中正规指

max μ_F(u) = 1 凸集合指曲线上任意两点之间，曲线上的任意一点所表示的隶属度都大于或等于两点中隶属度较小的一个，也即 μ_F(x) ≥ min { μ_F(a) , μ_F(b) } ∀ a,b ∈ U x ∈ [a,b]

模糊语言变量

模糊语言变量（FLV）表示一个或多个模糊集合的合成，定量地表示一种概念或域。例如
目标朝向 = { 远左，左，中，右，远右 }
它的隶属函数形状集合（或为模糊形，模糊表面）可以如下所示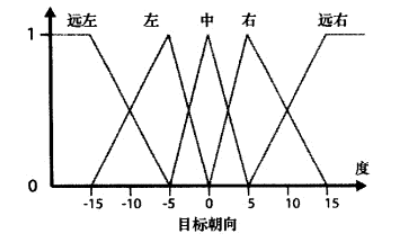

掠夺者中的模糊逻辑

了解完了基本概念，我们就可以看看如何在掠夺者中引入模糊集合来计算武器的期望分数。

模糊规则

传统的判断可能是这样的：
如果 Wizard.Health ≤ 0 那么 Wizard.Die()
但是模糊规则不同。在模糊系统中，判断可能是这样的：
如果 敌人受伤非常严重 那么 敌人逃跑

为武器设计模糊语言变量

设计模糊变量时，应当依据如下准则

• 通过模糊语言变量的任何垂直线，在每个与之相交的模糊集合的隶属度总和应为1。这保证了模糊形数值的平稳过渡。
• 通过模糊语言变量的任何垂直线，应当只与两个或更少的模糊集合相交。这保证了模糊形足够简单易用

例如使用火箭炮这一武器的期望取决于与敌人的距离和弹药量，其中模糊集合如下图所示：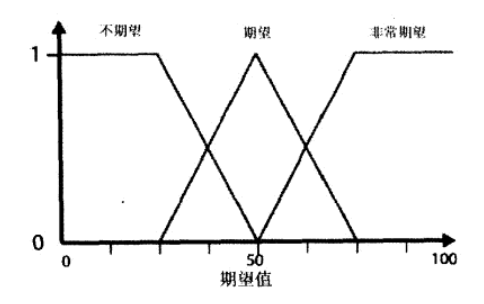

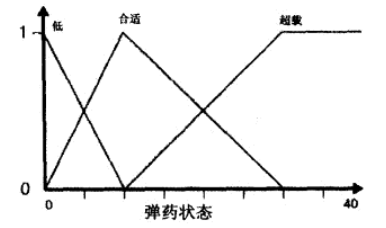
为武器设计模糊规则

由于游戏中假想的火箭炮是一种爆炸范围较大，弹道较慢的武器，所以可以设计规则如下所示：

1. 如果距离远且弹药超载，期望攻击
2. 如果距离远且弹药合适，不期望攻击
3. 如果距离远且弹药少，不期望攻击
4. 如果距离中等且弹药超载，非常期望攻击
5. 如果距离中等且弹药合适，非常期望攻击
6. 如果距离中等且弹药少，期望攻击
7. 如果距离近且弹药超载，不期望攻击
8. 如果距离近且弹药合适，不期望攻击
9. 如果距离近且弹药少，不期望攻击

模糊推理

引入这些花里胡哨的概念的目的在于根据这些模糊的规则与对应的隶属度函数，以一组输入得到一个确定的输出值。这一输出值即可作为期望分数，与其他武器的期望分数相比较，从而让AI角色选择合适的武器。于是，对于一组输入，我们需要以如下形式进行模糊推理：

• 对于每条规则，根据输入数据计算前提条件的隶属度
• 根据计算出的隶属度得到这一规则的推理结论隶属度
• 综合所有规则的结论，得到一个单一的结论
• 将结论去模糊化，得到期望分数

例如：
设输入条件中距离为200，弹药为8。
对于规则1，查阅上面的模糊形可知，距离200对于距离远的隶属度为0.33，弹药8对于子弹超载的隶属度为0。“且”这一连接词告知我们需要计算隶属度的交集，也即取值为min {0，0.33} = 0。所以这里规则1推导出的对期望攻击的隶属度为0。
类似地可以计算出，规则2推导出的对不期望攻击的隶属度为min {0.33,0.78} = 0.33。以此类推进行计算，结果可以归纳为如下一个矩阵，也即模糊联想矩阵（FAM）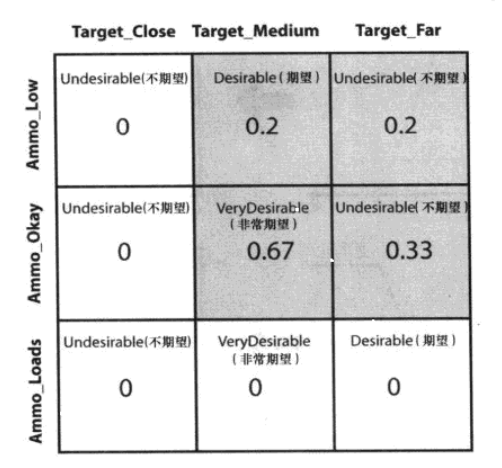

接下来，我们需要为这一矩阵得到一个单一的模糊集合结论。
首先，我们需要处理矩阵中的多重置信度，也即对于同一结论的好几个不同的隶属度，这里有两种常用的方案

• 取和并截断到最大值（也即1）
• 取最大值，也即“或”运算

这里我们采用第二种方案。可以得到如下的计算结果

结论	置信度
不期望攻击	0.33
期望攻击	0.2
非常期望攻击	0.67
接下来我们需要利用矩阵结果对原本的期望值模糊集合进行截断后合并处理。注意对比下图左侧的截断后结果与原本的期望值隶属度函数。
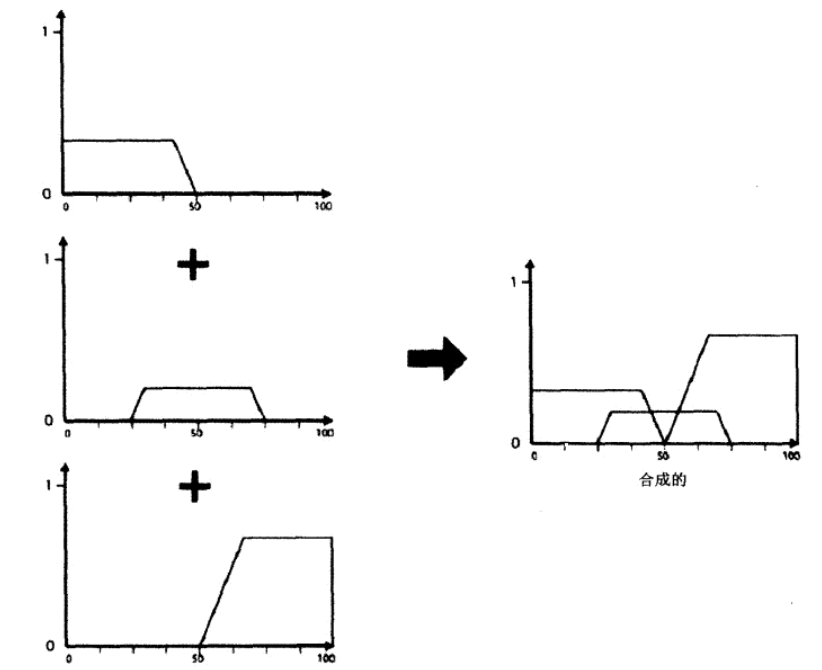于是我们便得到了对应这组输入的新的模糊形。
最后一步是利用模糊形得到一个期望分数，也即去模糊化。这里有以下几种方案。

• 最大值均值（MOM）
  这种算法的思路是计算具有最高置信度输出值的平均值。例如对于上面的合成模糊形，在右侧梯形的上方取到最值。而右侧梯形的左上顶点为66，右上顶点为100，便得到最大值均值83，作为期望分数。
  这一方法的问题是为了效率抛弃了左侧的大量数据。

• 中心法
  这是一种准确而复杂的方法。它的思路是通过采样大致确定模糊形的重心。其公式如下：
  
  其中，s是每个采样点的值，DOM(s)是对应的模糊语言变量的隶属度。显而易见，被取样值的越多，这一算法越准确。实践中通常使用10到20个采样点。
  例如对于上面的模糊语言变量，采样取10、20、30 …… 100，共计10个采样点。它们对应的隶属度分别为0.33、0.33、0.53、0.53、0.2、0.6、0.87、0.67、0.67、0.67（部分值为看图估计），故：
  Desirability = （10 * 0.33 + 20 * 0.33 + …… + 100 * 0.67）/（0.33 + 0.33 + …… + 0.67）
  也即 334.8/5.4 = 62

• 最大值平均
  这一方法的计算较为简单，而且结果接近于中心法，适合使用于实际的项目之中。
  一个模糊集合的最大值或代表值也就是对这个集合的隶属度为1的值。对于梯形集合而言，这意味着上方两顶点的平均值，退化为三角形时结论自然变为三角形上顶点。
  最大值平均（MaxAv）去模糊方法的公式如下：
  
  对于上述模糊形，计算过程如下：
  首先得到各个集合的代表值

  集合	代表值	置信度
  不期望攻击	12.5	0.33
  期望攻击	50	0.2
  非常期望攻击	87.5	0.67
  代入公式计算： Desirability = （1.25 * 0.33 + 50 * 0.2 + 87.5 * 0.67）/（0.33 + 0.2 + 0.67） = 72.75 / 1.2 = 60.625

于是我们便利用模糊逻辑得到了所需的期望分数，计算不同武器的期望分数即可作为AI的选择依据。

库博方法

在看到上面定义的模糊规则时，你可能已经想到，仅仅是两条三种情况的模糊语言变量，却产生了3 * 3 = 9条模糊规则。显而易见，模糊规则的数量会随着模糊语言变量的复杂度与数量飞速增加。幸运的是，库博方法可以解决这一问题。
库博方法通过拆解，使规则增加的速度降低为线性。其基于一个简单规则：
如果距离远且弹药超载，期望攻击 在逻辑上等价于
如果距离远，期望攻击
或 如果弹药超载，期望攻击
前述的9条规则在库博方法的简化后如下：

1. 如果距离近，不期望攻击
2. 如果距离中等，非常期望攻击
3. 如果距离远，不期望攻击
4. 如果弹药少，不期望攻击
5. 如果弹药合适，期望攻击
6. 如果弹药超载，非常期望攻击
   这一简化的方法并不直观，甚至完全变换了原本的规则。但神奇的是仅需变换规则本身而不用改变其余部分，代码即可适用于库博规则，其得到的期望分数与传统的模糊逻辑推理程序十分类似。例如前述规则使用库博规则后得到的期望分数为57.16，近似于之前的60.625。